Bedreigen kwantumcomputers moderne cryptografie?

Posted on: 10/05/2022 by: Kristof Verslype

Hoe hard moeten we ons zorgen maken dat kwantumcomputers de moderne cryptografie zullen ondergraven? Als we bepaalde schreeuwerige persberichten die een crypto-apocalypse prediken, mogen geloven, is het hoogtijd voor bestiale paniek.

Een eerste kanttekening is alvast dat quantum computing momenteel dermate gehypet is, dat zelfs experts zoals Sankar Das Sarma zich er ongemakkelijk bij voelen. In maart dit jaar schreef hij in een opinie voor MIT Technology Review:

I am as pro-quantum-computing as one can be: I’ve published more than 100 technical papers on the subject, and many of my PhD students and postdoctoral fellows are now well-known quantum computing practitioners all over the world. But I’m disturbed by some of the quantum computing hype I see these days, particularly when it comes to claims about how it will be commercialized.

In 2020 schreef ik uitgebreid over de kwantumcomputers ([1], [2]) en de dreiging die ervan uitgaat op de moderne cryptografie ([3], [4]). Ondertussen is het tijd voor een korte update op dat vlak. De stellingen van toen blijven onverkort geldig, maar kunnen nu wel concreter gemaakt worden.

In de eerste plaats is het moderne publieke sleutelcryptografie die bedreigd wordt. Dan spreken we over systemen gebaseerd op RSA of, recenter, elliptische krommen, die gebruikt worden voor onder meer het opzetten van veilige kanalen, authenticatie, digitale handtekeningen en ook hybride encryptie.

Een overzicht

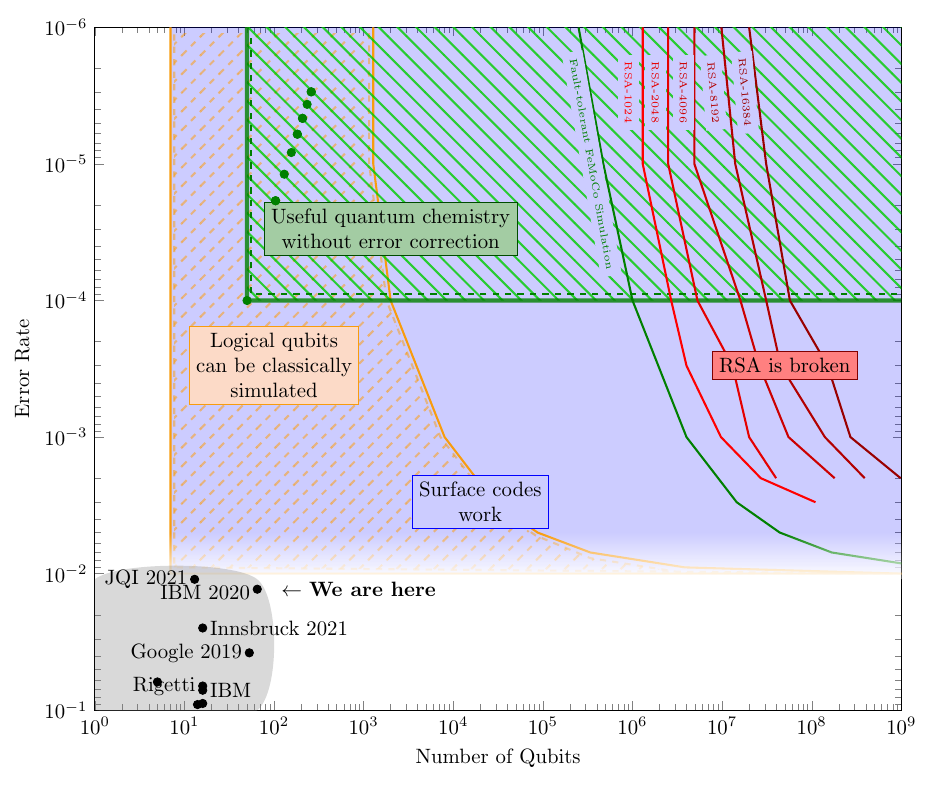
Onderstaande, weliswaar schetsmatige, figuur, gemaakt in 2021 door Samuel Jaques van de Universiteit van Oxford, is zeer verhelderend en geeft een idee van de weg die afgelegd moet worden richting kwantumcomputers die effectief een bedreiging vormen voor cryptosystemen gebaseerd op RSA. De krachtigste kwantumcomputer op het moment van schrijven is de IBM Eagle, met 127 (fysieke) qubits en werd eind 2021 aangekondigd. Om RSA te breken, met behulp van het algoritme van Shor, zijn echter minstens een paar tiental miljoen (fysieke) qubits nodig (X-as). Bovendien moet ook het foutenpercentage drastisch naar beneden (verticale as).

Men is het erover eens dat men qubits nooit volledig foutenvrij zal krijgen. Daarom zullen krachtige kwantumcomputers onvermijdelijk nood hebben aan errorcorrectie om de kwantumtoestanden van dergelijke machines voldoende lang coherent (correct) te houden. Bij foutencorrectie vormen meerdere (honderden, duizenden, honderduizenden) fysieke, onnauwkeurige qubits samen één logische, nauwkeurige qubit. Voor de duidelijkheid: de X-as toont het aantal vereiste fysieke qubits.

De blauwe zone is de zone waarbinnen die errorcorrectie mogelijk wordt. Op de figuur is te zien dat de qubits van de huidige generatie kwantumcomputers daarvoor nog onvoldoende nauwkeurig zijn (ze bevinden zich nog onder de blauwe zone), maar we komen wel in de buurt.

In de geel gearceerde zone kan een klassieke computer misschien niet langer die fysieke qubits simuleren, maar wel nog de logische qubits. In die zone is het aantal logische qubits inderdaad nog zeer beperkt.

De groene zone, ten slotte, is de zone waarbinnen bepaalde chemische problemen zonder errorcorrectie opgelost kunnen worden. Voor meer details verwijzen we naar het artikel van Samuel Jaques.

Op de figuur zien we dat er dus miljoenen tot tientallen miljoenen (fysieke) qubits nodig zijn om RSA te breken. Wat niet op de figuur staat, is dat ook voor het breken van elliptische krommen we moeten denken in termen van tientallen miljoenen (fysieke) qubits, zoals blijkt uit een recente publicatie. Daarin werd berekend dat een kwantumcomputer met bepaalde eigenschappen, waaronder 13 miljoen fysieke qubits, 256-bit sleutels zou kunnen kraken. Dit komt overeen met een 128 bit security, wat vandaag best als een ondergrens beschouwd wordt.

Exponentiële groei?

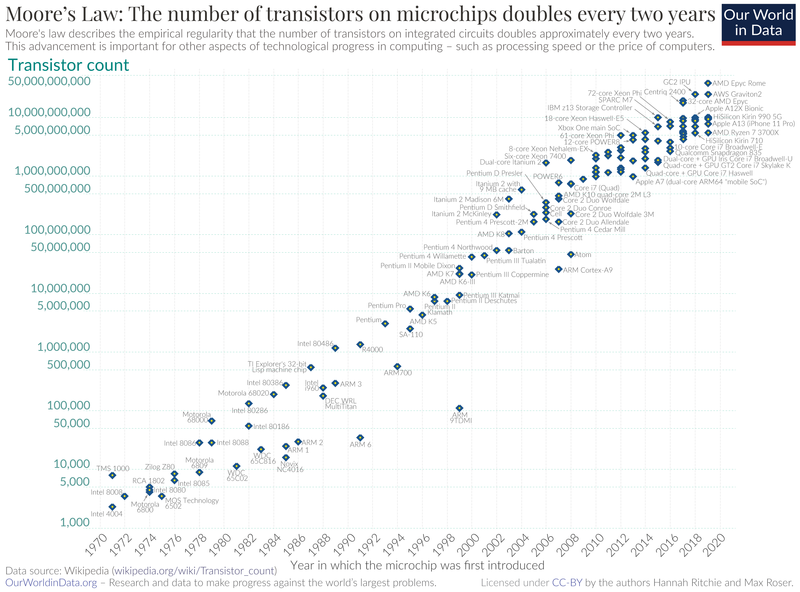
De kracht van klassieke computers kent sinds lange tijd een exponentiële groei. Deze historische tendens, waarbij het aantal schakelingen op een chip elke anderhalf tot twee jaar verdubbelt, wordt de wet van Moore genoemd en wordt geïllustreerd in onderstaande figuur. De term ‘wet’ is wat ongelukkig gekozen; het is geen natuurwet (en al helemaal geen juridische).

Het blijkt inderdaad moeilijker dan in het verleden om deze exponentiële groeit te handhaven en onvermijdelijk zal dit groeitempo ooit ophouden, niet in de laatste plaats omdat schakelingen op termijn zo klein worden dat ze in toenemende mate onderhevig worden aan kwantumeffecten. De Newtoniaanse fysica, waar klassieke computers op gebaseerd zijn, is dan niet langer van toepassing.

Indien kwantumcomputers ooit een bedreiging willen vormen voor de moderne cryptografie, is er eveneens een exponentiële groei nodig, die bovendien lang genoeg volgehouden moet kunnen worden. Het is allerminst zeker dat dit het geval zal zijn. De historische analogie met de wet van Moore, die al ruim 50 jaar standhoudt, ontbreekt elke wetenschappelijke basis en biedt dus geen garanties. Als we naar de roadmap van IBM kijken, lijken ze wel die ambitie te hebben, met onder meer een kwantumcomputer van meer dan 1000 qubits in 2023.

Omgaan met onzekerheid

Die onzekerheid wat betreft de evolutie van kwantumcomputers vinden we ook terug in communicatie van de NSA. De Amerikaanse inlichtingendienst stelt het als volgt:

NSA does not know when or even if a quantum computer of sufficient size and power to exploit public key cryptography will exist.

De NSA neemt echter geen risico en is van plan te migreren naar die nieuwe generatie publieke sleutelcryptografie, die op dit moment door het NIST, het National Institute for Standards and Technologies, gestandaardiseerd wordt. Een voldoende sterke kwantumcomputer zit er weliswaar niet onmiddellijk aan te komen, maar niettemin moet de NSA rekening houden met een zeer verre horizon, die meerdere decennia in de toekomst ligt:

The cryptographic systems that NSA produces, certifies, and supports often have very long lifecycles. NSA has to produce requirements today for systems that will be used for many decades in the future

New cryptography can take 20 years or more to be fully deployed to all National Security Systems

Conclusie

Dat is dan meteen ook de boodschap ter afronding van dit artikel. De data die vandaag beschermd wordt is binnen een aantal decennia misschien nog steeds gevoelig. Bovendien kost het migreren van systemen naar kwantumresistente alternatieven tijd. De crypto-apocalypse zit er niet meteen aan te komen en komt er misschien zelfs nooit. Dit neemt niet weg dat we beter het zekere voor het onzekere nemen en ons best vandaag reeds voorbereiden om vlot te kunnen migreren naar die nieuwe generatie publieke sleutelcryptografie die er zit aan te komen. Het NIST is inderdaad bezig met een standaardisatieprocedure, die met wat geluk dit of volgend jaar afgerond zal worden. De noodzaak tot migreren naar de nieuwe standaarden geldt in het bijzonder voor systemen die data verwerken die een lange tijd gevoelig blijven.

Dit is een ingezonden bijdrage van Kristof Verslype, cryptograaf bij Smals Research. Het werd geschreven in eigen naam en neemt geen standpunt in namens Smals.