Kwantumcomputers & cryptografie deel 3: De Crypto-apocalypse?

Welke impact zullen kwantumcomputers hebben op onze moderne cryptografie, die levensnoodzakelijk is in onze samenleving? Deze blogpost bespreekt de impact op symmetrische encryptie, op cryptografische hashfuncties en op publieke sleutelcryptografie.

Impact op symmetrische encryptie

Bij symmetrische encryptie gebeurt encryptie en decryptie met dezelfde sleutel (zie onderstaande figuur). AES (Advanced Encryption Standard) is vandaag de wereldwijde standaard, die ongeveer 20 jaar geleden ontwikkeld werd door de KU Leuven. Vandaag biedt een AES-sleutel die 256 bits lang is (AES-256) een veiligheid van 256 bits, wat wil zeggen dat er 2²⁵⁶ ≈ 10⁷⁷ (een 1 gevolgd door 77 nullen) mogelijke sleutels zijn. De efficiëntste aanval doet niet veel beter dan het één na één testen van alle mogelijke sleutels, tot de juiste gevonden is. Doordat de zoekruimte zo enorm groot is, is dit gewoon onbegonnen werk en zijn de kansen op succes verwaarloosbaar.

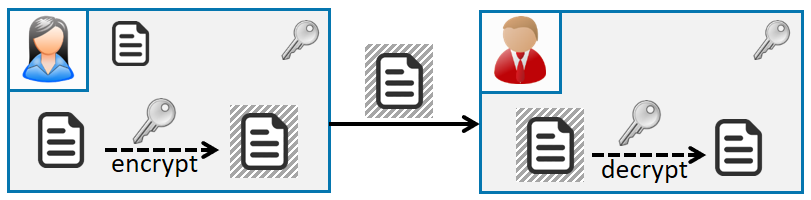
Encryptie en decryptie m.b.v. eenzelfde, gedeelde symmetrische sleutel.

In 1996 stelde Lov Grover echter een kwantumalgoritme (Grover’s algorithm) voor dat de zoekruimte om de inverse te berekenen van een blackbox functie verkleint van N tot 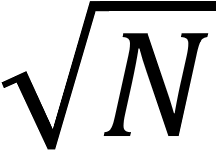, waarbij N het aantal mogelijke inputs (de zoekruimte) is. In het geval van symmetrische vercijfering bestaat die blackbox uit niet alleen het vercijferalgoritme, maar ook de symmetrische sleutel.

Het algoritme van Grover biedt daarmee een kwadratische versnelling voor het vinden van symmetrische sleutels. De zoekruimte van een AES-256 sleutel verkleint immers van 2²⁵⁶ ≈ 10⁷⁷ tot 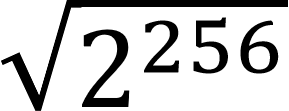= 2¹²⁸ ≈ 10³⁸ (een 1 gevolgd door 38 nullen). Om een zelfde veiligheidsniveau als vandaag te behouden in een tijdperk met krachtige kwantumcomputers, volstaat het dus om de sleutellengte te verdubbelen. Dat valt al bij al goed mee.

Om het algoritme van Grover uit te voeren zijn log₂(N) logische qubits vereist. Voor een AES-256 sleutel betekent dit 256 logische qubits. Onderzoekers berekenden in 2016 ook dat voor AES sleutels van 128, 192 en 256 bits respectievelijk 2953, 4449 en 6681 fysieke qubits vereist zijn. (Zie deel 2 in de reeks voor het onderscheid tussen logische en fysieke qubits.)

Het algoritme van Grover steunt op de aanname dat er reeds een orakel bestaat - een grote kwantum logische poort (zie deel 1) - dat meermaals toegepast wordt op de N (logische) qubits samen. Dit orakel is in feite een (kwantum)representatie van de blackbox. In werkelijkheid zal dit orakel afgeleid moeten worden uit de (klassieke) blackbox functie. Het is voor uw nederige auteur vooralsnog onduidelijk hoe deze voorbereidende stap sneller dan lineair uitgevoerd kan worden. Dit is nochtans een conditio sine qua non om kwantumcomputers zelfs nog maar in theorie een bedreiging te laten vormen voor symmetrische cryptografie.

Samengevat vormt het algoritme van Grover vandaag slechts op papier en onder een zware assumptie een bedreiging voor symmetrische encryptie. Het werd tot op heden nog niet op een kwantumcomputer uitgevoerd, zelfs niet met erg korte sleutels. Indien die bedreiging zich ooit zou concretiseren, kunnen we daar bovendien mee omgaan door de sleutellengte te verdubbelen.

Impact op cryptografische hashfuncties

Cryptografische hashfuncties laten toe een unieke fingerprint te berekenen van data, zonder dat die fingerprint informatie lekt over de originele data. Het is een cryptowerkpaard dat in de praktijk enorm vaak gebruikt wordt, bijvoorbeeld bij het plaatsen van digitale handtekeningen en bij het bouwen van blockchains. De output van eenzelfde hashfunctie (dus de fingerprint) heeft daarbij een vaste lengte, onafhankelijk van de grootte van de input.

Wanneer voor een cryptografische hashfunctie twee inputs gevonden worden die dezelfde output genereren, kan de cryptografische hashfunctie niet langer als veilig beschouwd worden. Voor de SHA1 hashfunctie – nog steeds in gebruik op vele eID kaarten – werd een dergelijke collision in 2017 gevonden. Dit alles heeft niets te maken met kwantumcomputers, maar toont wel aan hoe strikt men is voor cryptografische hashfuncties (en cryptografie in het algemeen), gezien het vaak een kwestie van tijd is voor een aanval die er op het eerste zicht misschien nogal onschuldig uitziet verder verfijnd wordt. Dat gebeurde dan ook in 2019 met de publicatie die een krachtigere en praktischere aanval beschrijft.

Een hashfunctie met een output van 256 bits heeft een veiligheid van 128 bits door de verjaardagenparadox, mits de aanvaller beschikt over voldoende schijfruimte om 2¹²⁸ hashwaarden te bewaren. Vandaag is zo’n aanval onhaalbaar.  

Door Grover’s algoritme te combineren met deze paradox daalt de veiligheid van een 256 bit hashfunctie van 128 naar tot 85 bit (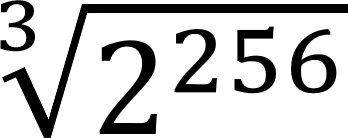 ≈ 2⁸⁵ ≈ 10²⁶) en wordt de aanval in dit geval dus een kleine 9000 miljard keer makkelijker. Meer algemeen zakt het veiligheidsniveau uitgedrukt in bits met twee derden. Voor dit alles zijn trouwens evenveel logische of fysieke qubits vereist als in de vorige sectie. Dus 256 logische qubits om SHA-256 te verzwakken of 6681 fysieke. Ook hier blijft de aanname van het bestaan van het kwantumorakel.

Samengevat volstaat het om de lengte van de uitvoer te verdriedubbelen om een zelfde veiligheidsniveau als vandaag te behouden in een tijdperk met krachtige kwantumcomputers. Ook hier valt best mee te leven.

Impact op publieke sleutelcryptografie

De grootste dreiging vanuit kwantumcomputers lijkt zich te situeren in de publieke sleutelcryptografie. Dat houdt in dat er gebruik gemaakt wordt van een sleutelpaar: een publieke sleutel die in principe door iedereen gekend mag zijn en een private sleutel die slechts door één entiteit gekend is. Dit wordt gebruikt voor digitale handtekeningen, authenticatie, het opzetten van veilige kanalen en vaak ook voor vercijfering (zie onderstaande figuur).

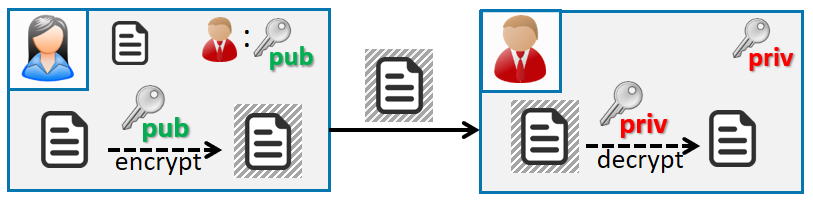
Encryptie met een publieke sleutel en decryptie met de corresponderende private sleutel.

In 1994 vond Peter Shor een kwantumalgoritme dat in staat is om efficiënt een getal te factoriseren, wat wil zeggen het ontbinden in zijn priemfactoren. Het getal 175 is bijvoorbeeld te ontbinden in 5 * 5 * 7. Voor klassieke computers is er daarvoor nog geen efficiënt algoritme gekend.

Hedendaags populaire sleutelcryptografie, meer bepaald RSA, is net gebaseerd op de veronderstelling dat dit probleem moeilijk is en blijft. Meer specifiek steunt RSA op de assumptie dat het onhaalbaar is om uit een groot getal dat het product is van twee half zo grote priemgetallen, opnieuw die priemgetallen te vinden. RSA zou dus gekraakt kunnen worden door een voldoende krachtige kwantumcomputer. RSA wordt vandaag nog intensief gebruikt. Onder meer uw Belgische elektronische identiteitskaart maakt er gebruik van, zowel voor digitale handtekeningen als voor authenticatie.

RSA werd voor het eerst voorgesteld in de jaren '70. Ondertussen wordt meer en meer, vooral sinds de eeuwwisseling, gemigreerd naar cryptografie gebaseerd op elliptische krommen (zie figuur voor een elliptische kromme in het reële vlak) omwille van de hogere efficiëntie en kortere sleutels. Punten op een dergelijke kromme kunnen opgeteld worden, wat resulteert in een nieuw punt op de kromme. Een punt P kan ook n keer (n een natuurlijk getal) met zichzelf opgeteld worden:  P’ = n . P. Cryptografie gebaseerd op elliptische krommen veronderstelt dat er geen efficiënt algoritme bestaat om uit P en P’ de waarde n te vinden. Dit noemt met het elliptic curve discrete logarithm problem, of kortweg ECDLP. Dit lijkt een totaal ander probleem dan dat waarop RSA steunt, maar toch zijn ze niet zo verschillend en kan het algoritme van Shor ook cryptografie gebaseerd op elliptische krommen breken.

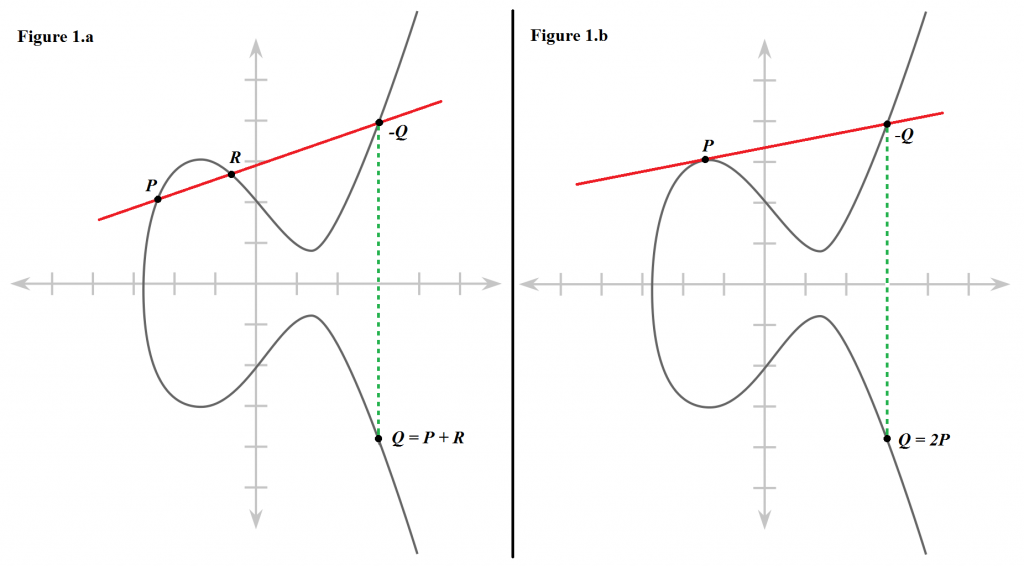
Optelling van punten op elliptishce krommen

De ironie wil dat door de kortere sleutellengte de modernere cryptografie gebaseerd op ECDLP met minder krachtige kwantumcomputers te kraken is dan oudere cryptografie gebaseerd op RSA. Er zijn bijvoorbeeld 1300 tot 1600 logische qubits nodig om een 224 bit EC sleutel te kraken. Dit biedt een gelijkaardige veiligheid als een 2048 bit RSA sleutel, dat pas gekraakt kan worden door een kwantumcomputer met 4096 qubits. Let wel, het gaat hier over logische qubits.

Zoals reeds aangegeven in het vorige artikel uit de reeks zijn er meerdere fysieke qubits nodig om één logische qubit te vormen. In 2019, zeer recent dus, hebben wetenschappers in detail berekend hoeveel fysieke qubits er nodig zijn om een 2048 bit RSA sleutel te kraken: Een kwantumcomputer met 20 miljoen fysieke qubits zou 8 uur moeten rekenen. Dit resultaat werd mogelijk gemaakt door verschillende optimalisaties aan het Shor algoritme. Schattingen uit 2012 gingen nog uit van 1 miljard fysieke qubits. Het is dus niet onwaarschijnlijk dat er in de toekomst benaderingen gevonden zullen worden die minder dan 20 miljoen qubits zullen vereisen.

Flash back naar vandaag. De krachtigste universele kwantumcomputer vandaag heeft 72 qubits en het grootste getal dat een kwantumcomputer met behulp van het algoritme van Shor heeft kunnen factoriseren is 21 en dateert van 2011. Ondertussen zijn naast het algoritme van Shor ook andere kwantumalgoritmes om twee getallen te factoriseren. Daarbij wordt het factorisatieprobleem omgevormt naar een optimalisatieprobleem. Dat is waar de adiabatische kwantumcomputers van D-Wave goed in zijn. Ze zijn makkelijker te bouwen maar zijn ook minder krachtig dan universele kwantumcomputers met evenveel qubits. Onderzoekers slaagden er in 2017 in om het getal 291311 te factoriseren in 523 en 557 op een de D-Wave 2X machine met ruim 1000 qubits. Echter, deze methode is vooral sterk wanneer de twee priemfactoren in hun binaire voorstelling slechts weinig verschillen. In het geval van 523 en 557 is de binaire voorstelling 1000001011 en 1000101101 die inderdaad in slechts drie bits van elkaar verschillen. Door de priemfactoren zorgvuldig te kiezen kunnen we het een dergelijke kwantumcomputer alvast een pak lastiger maken.

Ter vergelijking: klassieke computers slaagden er in februari 2020 in om het getal genaamd RSA-250 te factoriseren, wat bestaat uit 250 decimalen (821 bits).

Conclusie

Op het eerste zicht lijken symmetrische encryptie en cryptografische hashfuncties beter bestand tegen kwantumcomputers dan publieke sleutelencryptie. Een voldoende krachtige kwantumcomputer kan in een korte tijd een RSA of EC sleutel kraken, terwijl de lengte van AES sleutels gewoon verdubbeld moet worden om een zelfde veiligheid te behouden in een kwantumtijdperk. Wanneer we echter kijken naar het aantal vereiste qubits, dan merken we dat AES veel vroeger geaffecteerd zal worden. Een kwantumcomputer met 6681 qubits kan AES-256 sleutels verzwakken, terwijl we een kwantumcomputer nodig hebben van 20 miljoen bits om RSA-2048 sleutels te kraken. Qua veiligheid komt een RSA-2048 sleutel volgens o.a. het NIST trouwens slechts overeen met AES-112 en biedt het dus slechts 112 bits veiligheid.

Gegeven dat vandaag de krachtigste universele kwantumcomputer 72 qubits bevat en gegeven de exponentiële complexiteitstoename van kwantumcomputers met het aantal qubits, lijkt de bedreiging van de moderne cryptografie door kwantumcomputers toch wat verderaf te zijn dat wat veelal wordt aangenomen.

Toch blijft het onmogelijk te voorspellen wat de toestand binnen een aantal decennia zal zijn, terwijl gegevens die vandaag met behulp van cryptografie beschermd worden (at rest of in transit), dan nog steeds gevoelig kunnen zijn. In ons vierde en laatste deel leest u binnenkort gelukkig welke stappen er ondernomen worden onze gegevens en communicatie veilig te houden in geval men er ooit in slaagt krachtige kwantumcomputers te bouwen. Want, zo redeneert men bij zaken die men moeilijk kan inschatten, better safe than sorry.

Dit is een ingezonden bijdrage van Kristof Verslype, cryptograaf bij Smals Research. Het werd geschreven in eigen naam en neemt geen standpunt in namens Smals.